chillimath.com

chillimath

Menu

9. ABCD is a trapezium in which AB || DC and its diagonals intersect each other at the point O.

Triangles

Exercise 6.2

Ncert Solutions Class 10 Chapter 6 Triangles Exercise 6.2 Question 9
Previous
Next

Class 10

Triangles

Exercise 6.2

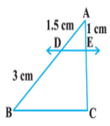
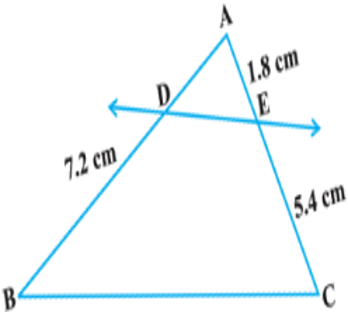
1. In Fig. (i) and (ii), DE || BC. Find EC in (i) AD in (ii).

2. E and F are points on the sides PQ and PR respectively of a ΔPQR. State whether EF || QR, if:
(i) PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm and FR = 2.4 cm.
(ii) PE = 4 cm, QE = 4.5 cm, PF = 8 cm and RF = 9 cm.
(iii) PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm.

3. In Figure, if LM || CB and LN || CD, prove that \(\frac{AM}{AB}=\frac{AN}{AD}\).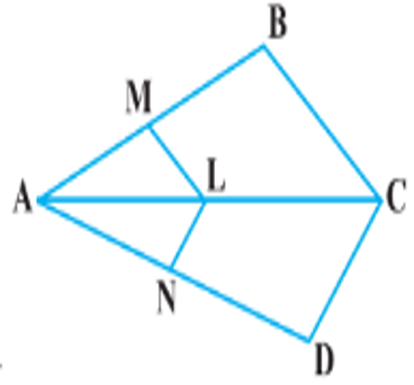

4. In Figure, DE || AC and DF || AE. Prove that \(\frac{BF}{FE}=\frac{BE}{EC}\).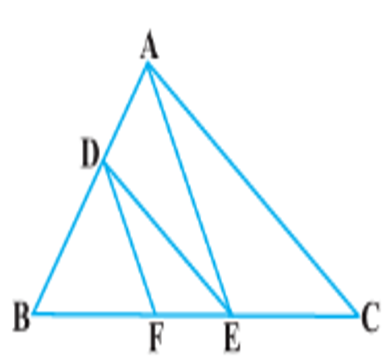

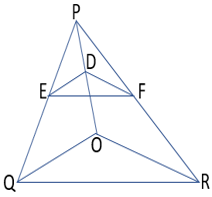
5. In Figure, DE || OQ and DF || OR. Show that EF || QR.

6. In Figure, A, B and C are points on OP, OQ and OR respectively such that AB || PQ and AC || PR. Show that BC || QR.

7. Using Basic Proportionality Theorem, prove that a line drawn through the mid-point of one side of a triangle parallel to another side bisects the third side. (Recall that you have proved it in Class IX).

8. Using Converse of Basic Proportionality Theorem, prove that the line joining the mid-points of any two sides of a triangle is parallel to the third side. (Recall that you have done it in Class IX).

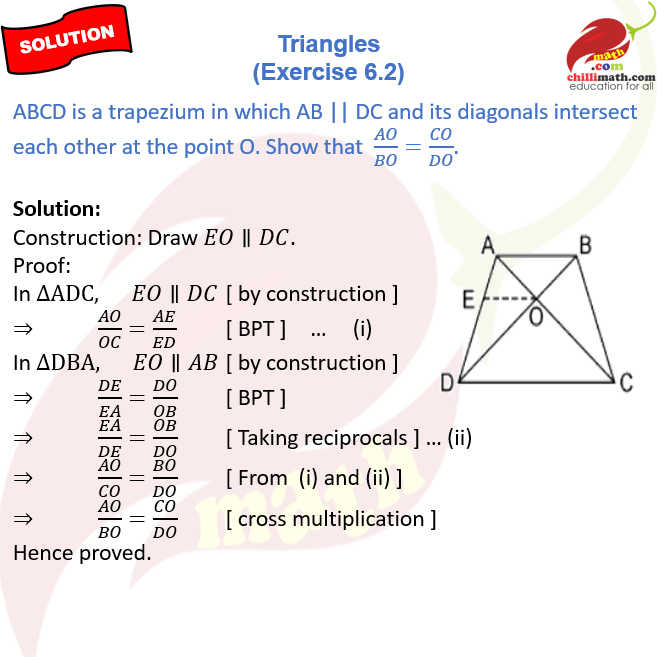
9. ABCD is a trapezium in which AB || DC and its diagonals intersect each other at the point O.

10. The diagonals of a quadrilateral ABCD intersect each other at the point O such that \(\frac{AO}{BO}=\frac{CO}{DO}\)⋅