Menu
Class 10
Triangles
Exercise 6.2
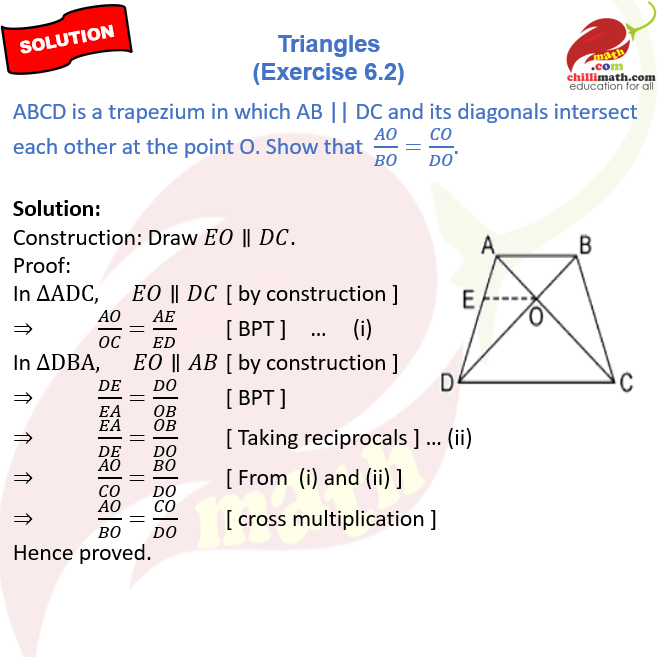
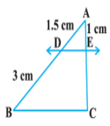
1. In Fig. (i) and (ii), DE || BC. Find EC in (i) AD in (ii).
2. E and F are points on the sides PQ and PR respectively of a ΔPQR. State whether EF || QR, if:
(i) PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm and FR = 2.4 cm.
(ii) PE = 4 cm, QE = 4.5 cm, PF = 8 cm and RF = 9 cm.
(iii) PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm.
3. In Figure, if LM || CB and LN || CD, prove that \(\frac{AM}{AB}=\frac{AN}{AD}\).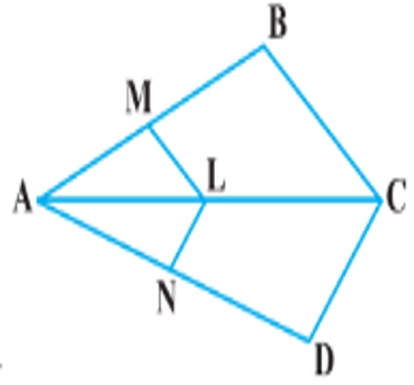
4. In Figure, DE || AC and DF || AE. Prove that \(\frac{BF}{FE}=\frac{BE}{EC}\).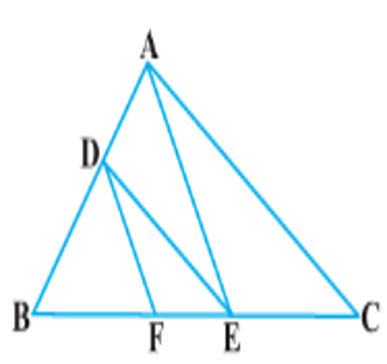
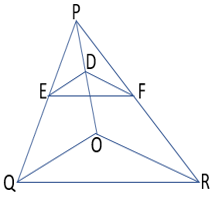
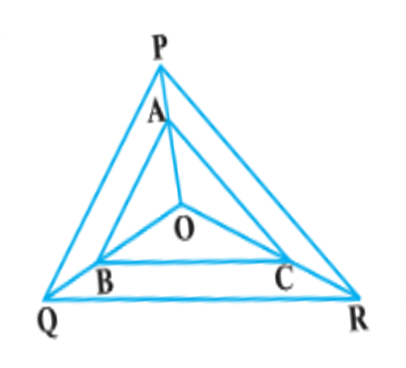
5. In Figure, DE || OQ and DF || OR. Show that EF || QR.
9. ABCD is a trapezium in which AB || DC and its diagonals intersect each other at the point O.