chillimath.com

chillimath

Menu

6. In Fig., AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.

class 9 chapter 7 Triangles exercise 7.1 question 6

 

Triangles

Exercise 7.1

Ncert Solutions Class 9 Chapter 7 Triangles Exercise 7.1 Question 6
Previous
Next

Class 9

Triangles

Exercise 7.1

1. In quadrilateral ACBD, AC = AD and AB bisects ∠A (see Fig.). Show that ΔABC ≅ ΔABD. What can you say about BC and BD?

class 9 chapter 7 Triangles exercise 7.1 question 1

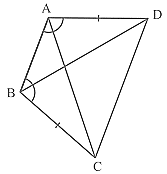
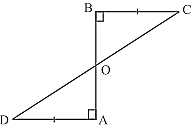
2. ABCD is a quadrilateral in which AD = BC and ∠DAB = ∠CBA (see Fig.). Prove that

(i) ΔABD ≅ ΔBAC

(ii) BD = AC

(iii) ∠ABD = ∠BAC.

class 9 chapter 7 Triangles exercise 7.1 question 2

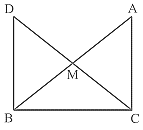
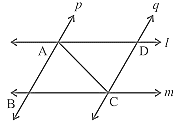
3. AD and BC are equal perpendiculars to a line segment AB (see Fig.). Show that CD bisects AB.

class 9 chapter 7 Triangles exercise 7.1 question 3

4. l and m are two parallel lines intersected by another pair of parallel lines p and q (see Fig.). Show that ΔABC ≅ ΔCDA.

class 9 chapter 7 Triangles exercise 7.1 question 4

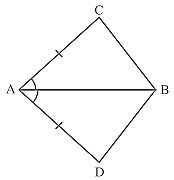
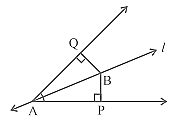
5. Line l is the bisector of an angle ∠A and B is any point on l. BP and BQ are perpendiculars from B to the arms of ∠A (see Fig.). Show that:
(i) ΔAPB ≅ ΔAQB
(ii) BP = BQ or B is equidistant from the arms of  ∠A.

class 9 chapter 7 Triangles exercise 7.1 question 5

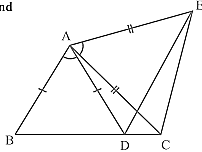
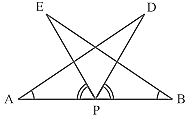
6. In Fig., AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.

class 9 chapter 7 Triangles exercise 7.1 question 6

7. AB is a line segment and  P is its mid-point. D and E are points on the same side of AB such that ∠BAD = ∠ABE and ∠EPA = ∠DPB (see Fig.). Show that:

(i) ΔDAP ≅ ΔEBP

(ii) AD = BE

class 9 chapter 7 Triangles exercise 7.1 question 7

8. In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see Fig.). Show that:

(i) ΔAMC ≅ ΔBMD

(ii) ∠DBC is a right angle.

(iii) ΔDBC ≅ ΔACB

(iv) CM=\(\frac{1}{2}\)AB.

class 9 chapter 7 Triangles exercise 7.1 question 8