Class 11
Relations and Functions
Miscellaneous Exercise
1. The relation f is defined by
Show that f is a function and g is not a function.
2. If \(f(x)=x^2\), find \(\frac{f(1.1)-f(1)}{(1.1-1)}\).
3. Find the domain of the function \(f\left(x\right)=\frac{x^2+2x+1}{x^2-8x+12}\).
4. Find the domain and the range of the real function f defined by \(f\left(x\right)=\sqrt{x-1}\).
5. Find the domain and the range of the real function f defined by \(f(x)=\left|x-1\right|\).
9. Let R be a relation from N to N defined by R={\((a,b) : a, b\in N\) and \(a=b^2\)}. Are the following true?
(i) \((a,a) \in R\), for all \(a\in N\)
(ii) \((a,b) \in R\), implies \((b,a) \in R\)
(iii) \((a,b) \in R, (b,c) \in R\) implies \((a,c) \in R\).
Justify your answer in each case.
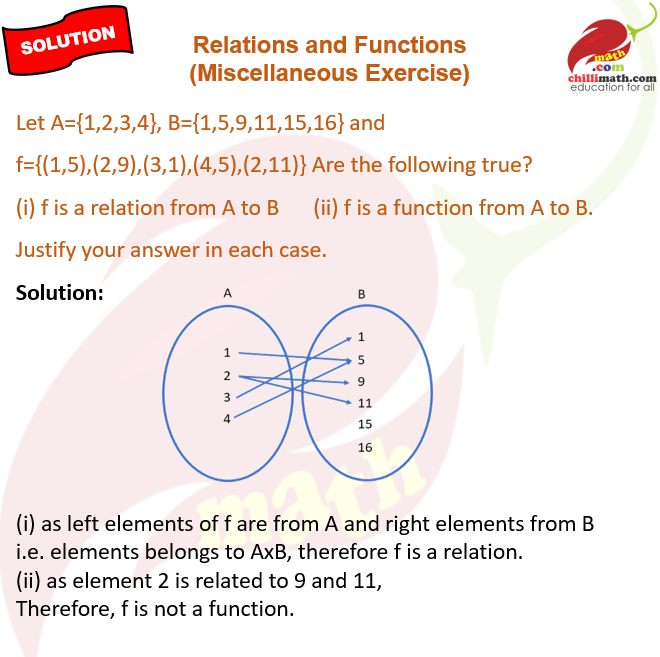
10. Let A={1,2,3,4}, B={1,5,9,11,15,16} and f={(1,5),(2,9),(3,1),(4,5),(2,11)}
(i) f is a relation from A to B
(ii) f is a function from A to B.
Justify your answer in each case.
12. Let A={9,10,11,12,13} and let f : A \(\rightarrow\) N be defined by f(n)=the highest prime factor of n. Find the range of f.