Ncert Solutions for Class 9
Number Systems
Number Systems
Exercise 1.1
Number Systems
Exercise 1.2
1. State whether the following statements are true or false. Justify your answers.
(i) Every irrational number is a real number.
(ii) Every point on the number line is of the form \(\sqrt{m}\), where m is a natural number.
(iii) Every real number is an irrational number.
3. Show how \(\sqrt5\) can be represented on the number line.
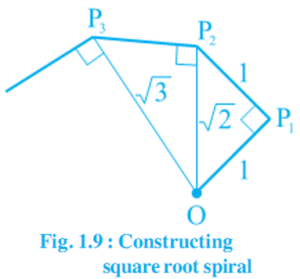
4. Classroom activity (Constructing the ‘square root spiral’) : Take a large sheet of paper and construct the square root spiral in the following fashion. Start with a point O and draw a line segment OP1 of unit length. Draw a line segment P1P2 perpendicular to OP1 of unit length (see Fig. 1.9). Now draw a line segment P2P3 perpendicular to OP2. Then draw a line segment P3P4 perpendicular to OP3. Continuing in this manner, you can get the line segment Pn-1Pn by drawing a line segment of unit length perpendicular to OPn-1. In this manner, you will have created the points P2, P3,…., Pn, … ., and joined them to create a beautiful spiral depicting \(\sqrt 2\), \(\sqrt 3\), \(\sqrt 4\), …
Number Systems
Exercise 1.3
1. Write the following in decimal form and say what kind of decimal expansion each has:
3. Express the following in the form \(p\over q\), where p and q are integers and q ≠ 0.
7. Write three numbers whose decimal expansions are non-terminating non-recurring.
9. Classify the following numbers as rational or irrational:
Number Systems
Exercise 1.4
1. Classify the following numbers as rational or irrational:
(ii) \((3+\sqrt{23})-\sqrt{23}\)
(iii) \({2\sqrt 7}\over{7\sqrt 7}\)
2. Simplify each of the following expressions:
(i) \((3+\sqrt 3)(2+\sqrt 2)\)
(ii) \((3+\sqrt 3)(3-\sqrt 3)\)
(iv) \((\sqrt 5-\sqrt 2)(\sqrt 5+\sqrt 2)\)
4. Represent \(\sqrt {9.3}\) on the number line.
5. Rationalise the denominators of the following:
(ii) \(1\over{\sqrt 7-\sqrt 6}\)
