1. Find the transpose of each of the following matrices:
(i) \(\begin{bmatrix}5 \\ {1\over 2}\\-1 \end{bmatrix}\)
(ii) \(\begin{bmatrix}1 &-1 \\ 2 & 3 \end{bmatrix}\)
(iii) \(\begin{bmatrix}-1 & 5 & 6 \\ {\sqrt 3} & 5 & 6 \\2 & 3 & -1\end{bmatrix}\)
Class 12
Matrices
Exercise 3.3
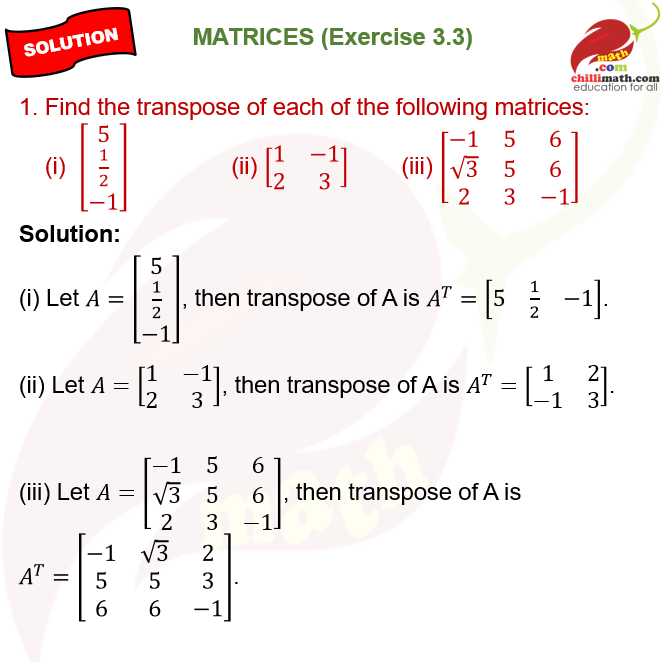
1. Find the transpose of each of the following matrices:
(i) \(\begin{bmatrix}5 \\ {1\over 2}\\-1 \end{bmatrix}\)
(ii) \(\begin{bmatrix}1 &-1 \\ 2 & 3 \end{bmatrix}\)
(iii) \(\begin{bmatrix}-1 & 5 & 6 \\ {\sqrt 3} & 5 & 6 \\2 & 3 & -1\end{bmatrix}\)
5. For the matrices A and B, verify that (AB)′ = B′A′, where
(i) \(A=\begin{bmatrix}1 \\ -4 \\ 3 \end{bmatrix}\), \(B=\begin{bmatrix}-1 & 2 & 1\end{bmatrix}\)
(ii) \(A=\begin{bmatrix}0 \\ 1 \\ 2 \end{bmatrix}\), \(B=\begin{bmatrix}1 & 5 & 7\end{bmatrix}\)
6. (i) If \(A=\begin{bmatrix}cosα & sinα \\ -sinα & cosα \end{bmatrix}\), then verify that A’A=I.
(ii) If \(A=\begin{bmatrix}sinα & cosα \\ -cosα & sinα \end{bmatrix}\), then verify that A’A=I.
8. For the matrix \(A=\begin{bmatrix}1 & 5 \\ 6 & 7 \end{bmatrix}\), verify that
(i) (A+A’) is a symmetric matrix
(ii) (A-A’) is a skew symmetric matrix.
10. Express the following matrices as the sum of a symmetric and a skew symmetric
matrix:
(i) \(\begin{bmatrix}3 & 5 \\ 1 & -1 \end{bmatrix}\)
(ii) \(\begin{bmatrix}6 & -2 & 2 \\ -2 & 3 & -1 \\ 2 & -1 & 3 \end{bmatrix}\)
(iii) \(\begin{bmatrix}3 & 3 & -1 \\ -2 & -2 & 1 \\ -4 & -5 & 2 \end{bmatrix}\)
(iv) \(\begin{bmatrix}1 & 5 \\ -1 & 2 \end{bmatrix}\).
Choose the correct answer in the Exercises 11 and 12.
11. If A, B are symmetric matrices of same order, then AB – BA is a
(A) Skew symmetric matrix
(B) Symmetric matrix
(C) Zero matrix
(D) Identity matrix